CG形状一覧
EGSで使用できるCG体系は以下に示す14種類です。
XYZについて指定した範囲を有する四角形を作成します。
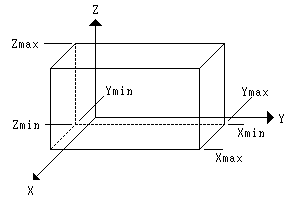
[ 形式 ] Xmin(1) Xmax(2) Ymin(3) Ymax(4) Zmin(5) Zmax(6)
(注) ( )内の数字は体系データ入力画面のパラメータ入力番号を示します。(1)ならば表中1番の行に入力します。(以降同じ)
Xmin,Xmax : X方向の最小値と最大値
Ymin,Ymax : Y方向の最小値と最大値
Zmin,Zmax : Z方向の最小値と最大値
[入力例]
形状番号1は(-10,-10,-10)から(10,10,10)の範囲を持つ四角形
形状番号2はXが0-5、Yが0-8、Zが0〜20の範囲を持つ四角形

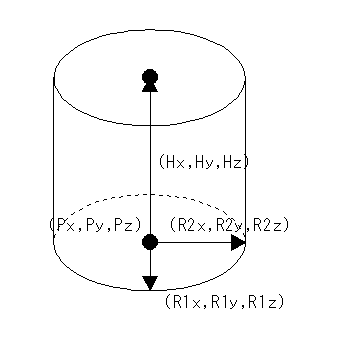
基準点Pを中心に半径Rで作成される円をベクトルH方向に沿って移動した跡にできる円柱を作成します。
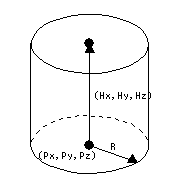
[ 形式 ] Px(1) Py(2) Pz(3) Hx(4) Hy(5) Hz(6) R(7)
Px,Py,Pz : 基準点となる円の中心X,Y,Z座標
Hx,Hy,Hz : 円柱の高さ方向のX,Y,Zベクトル (マイナスも入力可。円柱の高さは√(Hx×Hx+Hy×Hy+Hz×Hz)となる)
R : 円の半径
[入力例]
形状番号1は基準点が(0,0,0)座標からZ軸方向に10伸びた半径3の円柱
形状番号2は基準点が(0,0,0)座標からXとZ軸の間45°方向に14.14伸びた半径2の円柱

基準点Pを中心に半径Rで作成される球を作成します。
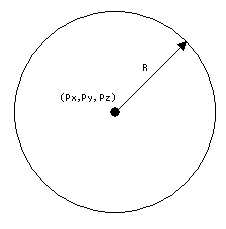
[ 形式 ] Px(1) Py(2) Pz(3) R(4)
Px,Py,Pz : 基準点となる球の中心X,Y,Z座標
R : 球の半径
[入力例]
形状番号1は基準点が(0,0,0)で半径10の球
形状番号2は基準点が(1,2,3)で半径5の球

基準点Pを中心に半径R1で作成される円をベクトルH方向に沿って半径R2になるように移動した跡にできる円錐を作成します。
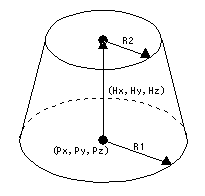
[ 形式 ] Px(1) Py(2) Pz(3) Hx(4) Hy(5) Hz(6) R1(7) R2(8)
Px,Py,Pz : 基準点となる円の中心X,Y,Z座標
Hx,Hy,Hz : 円錐の高さ方向のX,Y,Zベクトル(マイナスも入力可。円錐の高さは√(Hx×Hx+Hy×Hy+Hz×Hz)となる)
R1 : 円錐基準面の半径
R2 : 円錐ベクトル面の半径
[入力例]
形状番号1は基準点が(0,0,0)座標からZ軸方向に10伸びた基準面半径3のベクトル面半径1の円錐
形状番号2は基準点が(0,0,0)座標からXとZ軸の間45°方向に14.14伸びた基準面半径3のベクトル面半径1の円錐

基準点Pから半径R1の円に沿って半径R2の円を移動した跡にできるトーラスを作成します。トーラスは必ずXYZのいずれかの軸に平行であり、th1,th2で有効範囲を指定することができます。
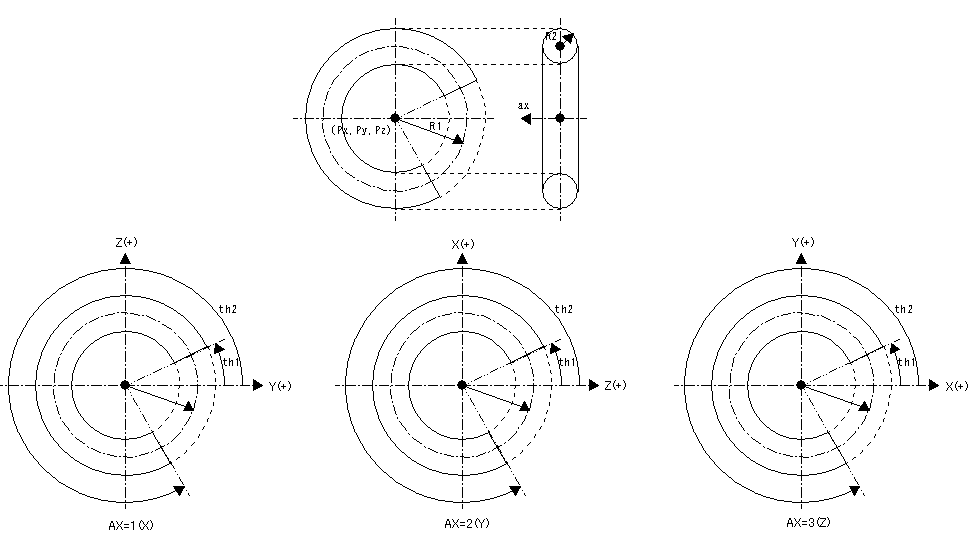
[ 形式 ] Px(1) Py(2) Pz(3) R1(4) R2(5) th1(6) th2(7) ax(8)
Px,Py,Pz : 基準点となるトーラスの中心X,Y,Z座標
R1 : トーラスの輪の半径
R2 : トーラスの管の半径
th1,th2 : トーラスの開始角度、終了角度(度(Degree)で入力)(0〜360の場合は切れ目のないトーラスとなる)
ax : トーラスの輪の中心軸(1=X軸 2=Y軸 3=Z軸)
[入力例]
形状番号1は基準点が(0,0,0)座標からX軸に沿う切れ目のないトーラス
形状番号2は基準点が(0,0,0)座標からX軸に沿う半分のトーラス

基準点PとベクトルA1とA2の辺で形成される四角形をベクトルA3方向に沿って移動した跡にできる四角柱を作成します。ただし、A1,A2,A3のベクトルは互いに直行していること。
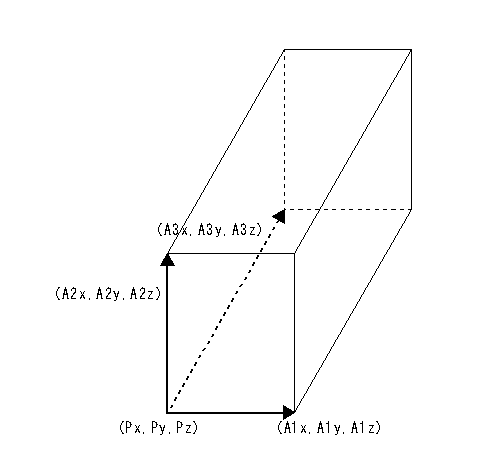
[ 形式 ] Px(1) Py(2) Pz(3) A1x(4) A1y(5) A1z(6) A2x(7) A2y(8) A2z(9) A3x(10) A3y(11) A3z(12)
Px,Py,Pz : 基準点となる頂点のX,Y,Z座標
A1x,A1y,A1z : 基準点から延ばした辺1のX,Y,Zベクトル
A2x,A2y,A2z : 基準点から延ばした辺2のX,Y,Zベクトル
A3x,A3y,A3z : 基準点から延ばした辺3のX,Y,Zベクトル
[入力例]
形状番号1は基準点が(0,0,0)座標で□10がZ軸に10延びた四角柱
形状番号2は基準点が(0,0,0)座標でZ軸を中心に45度回転している□10がZ軸に10延びた四角柱

基準点Pを中心に短軸R1と長軸R2で作成される楕円をベクトルH方向に沿って移動した跡にできる楕円柱を作成します。
[ 形式 ] Px(1) Py(2) Pz(3) Hx(4) Hy(5) Hz(6) R1x(7) R1y(8) R1z(9) R2x(10) R2y(11) R3z(12)
Px,Py,Pz : 基準点となる楕円の中心X,Y,Z座標
Hx,Hy,Hz : 楕円柱の高さ方向のX,Y,Zベクトル (マイナスも入力可。円柱の高さは√(Hx×Hx+Hy×Hy+Hz×Hz)となる)
R1x,R1y,R1z : 楕円の短軸を示すX,Y,Zベクトル
R2x,R2y,R2z : 楕円の長軸を示すX,Y,Zベクトル
[入力例]
形状番号1は基準点が(0,0,0)でZ軸に平行な楕円柱(短軸はX軸方向)
形状番号2は基準点が(0,0,0)でZ軸に平行な楕円柱(短軸はXとY軸の間45°方向)

基準点Pを中心に短軸R1と長軸R2で作成される楕円をベクトルH方向に沿って比率wの楕円に移動した跡にできる楕円錐を作成します。
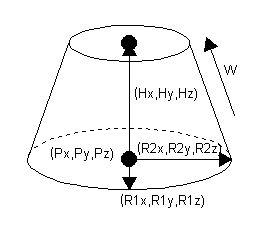
[ 形式 ] Px(1) Py(2) Pz(3) Hx(4) Hy(5) Hz(6) R1x(7) R1y(8) R1z(9) R2x(10) R2y(11) R3z(12) w(13)
Px,Py,Pz : 基準点となる楕円の中心X,Y,Z座標
Hx,Hy,Hz : 楕円柱の高さ方向のX,Y,Zベクトル (マイナスも入力可。円柱の高さは√(Hx×Hx+Hy×Hy+Hz×Hz)となる)
R1x,R1y,R1z : 楕円の短軸を示すX,Y,Zベクトル
R2x,R2y,R2z : 楕円の長軸を示すX,Y,Zベクトル
w : 楕円の比率
[入力例]
形状番号1は基準点が(0,0,0)でZ軸に平行な楕円柱(短軸はX軸方向) 比率0.5
形状番号2は基準点が(0,0,0)でZ軸に平行な楕円柱(短軸はXとY軸の間45°方向) 比率2.0

焦点座標P1とP2主軸Rの長さが一定の距離を保つ軌跡でできる楕円球を作成します。
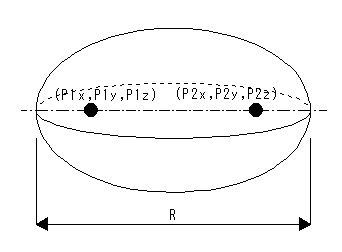
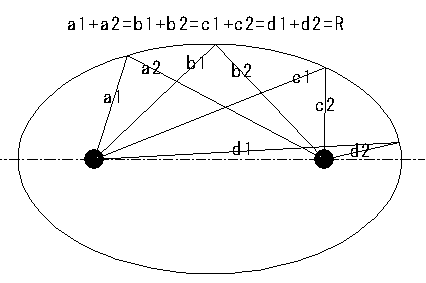
[ 形式 ] P1x(1) P1y(2) P1z(3) P2x(4) P2y(5) P2z(6) R(7)
P1x,P1y,P1z : 1つ目の焦点座標(X,Y,Z)
P2x,P2y,P2z : 2つ目の焦点座標(X,Y,Z)
R : 主軸の長さ
[入力例]
形状番号1は焦点座標が(-5,0,0)と(5,0,0)のX軸に平行な楕円球
形状番号2は焦点座標が(0,0,0)と(10,10,0)のXとY軸の間45°方向に平行な楕円球

基準点PとベクトルA1とA2の辺で形成される三角形をベクトルA3方向に沿って移動した跡にできる三角柱を作成します。ただし、A1,A2,A3のベクトルは互いに直行していること。
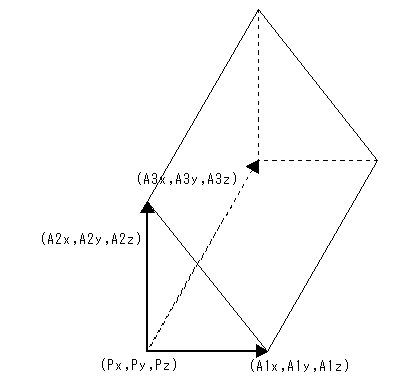
[ 形式 ] Px(1) Py(2) Pz(3) A1x(4) A1y(5) A1z(6) A2x(7) A2y(8) A2z(9) A3x(10) A3y(11) A3z(12)
Px,Py,Pz : 基準点となる頂点のX,Y,Z座標
A1x,A1y,A1z: 基準点から延ばした三角形辺1のX,Y,Zベクトル
A2x,A2y,A2z: 基準点から延ばした三角形辺2のX,Y,Zベクトル
A3x,A3y,A3z: 基準点から延ばした高さのX,Y,Zベクトル
[入力例]
形状番号1は基準点が(0,0,0)でベクトル(5,0,0)と(0,10,0)で形成される三角形をZ軸に10延ばした三角柱
形状番号2は基準点が(0,0,0)でベクトル(5,1,0)と(2,10,0)で形成される三角形をZ軸に10延ばした三角柱

任意の4,5または6面体。頂点のXYZ座標P1〜P8を指定し、面データS1〜S6を十進数で表した4桁の整数で指定する。4桁の整数は各桁が面の頂点番号を示し、順序は任意とする。4点より少ない頂点で構成される面は余りの頂点番号に0を入力する。使用しない頂点座標はXYZに0を入力する。
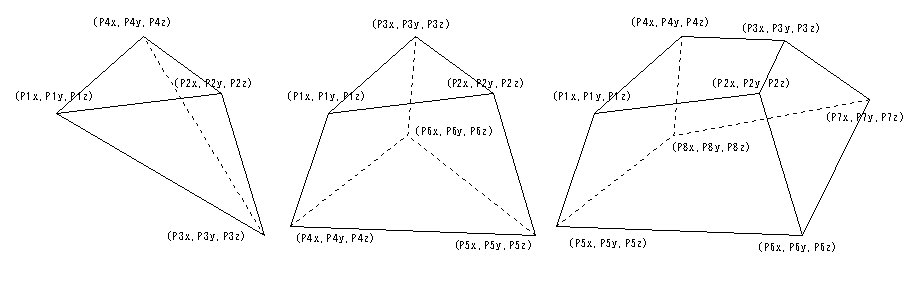
[ 形式 ] P1x(1) P1y(2) P1z(3) P2x(4) P2y(5) P2z(6) P3x(7) P3y(8) P3z(9) P4x(10)
P4y(11) P4z(12) P5x(13) P5y(14) P5z(15) P6x(16) P6y(17) P6z(18) P7x(19) P7y(20)
P7z(21) P8x(22) P8y(23) P8z(24) S1(25) S2(26) S3(27) S4(28) S5(29) S6(30)
P1x,P1y,P1z : 頂点1のX,Y,Z座標
P2x,P2y,P2z : 頂点2のX,Y,Z座標
P3x,P3y,P3z : 頂点3のX,Y,Z座標
P4x,P4y,P4z : 頂点4のX,Y,Z座標
P5x,P5y,P5z : 頂点5のX,Y,Z座標
P6x,P6y,P6z : 頂点6のX,Y,Z座標
P7x,P7y,P7z : 頂点7のX,Y,Z座標
P8x,P8y,P8z : 頂点8のX,Y,Z座標
S1,S2,S3,S4,S5,S6 : 6つの面を記述する4桁の整数。4桁の整数は各桁が面の頂点番号を示し、順序は任意とする。4点より少ない頂点で構成される面は余りの頂点番号に0を入力する。
[入力例]
形状番号1は頂点数8つの6面体
形状番号2は頂点数6つの5面体
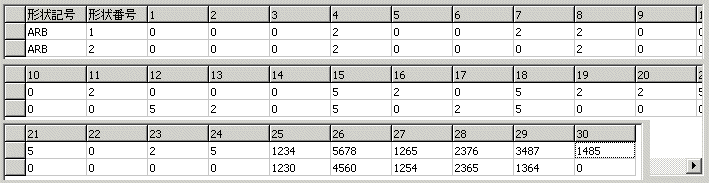
指定したベクトルN方向を領域とする半空間を作成する。
[ 形式 ] Nx(1) Ny(2) Nz(3) L(4)
Nx,Ny,Nz : 内側領域を示すベクトルX,Y,Z (マイナスも入力可)
L : ベクトルNに沿った原点(0,0,0)から平面までの距離 (マイナスも入力可)
[入力例]
形状番号1はZ=5から上が領域となる半空間
形状番号2はZ=-5から下が領域となる半空間

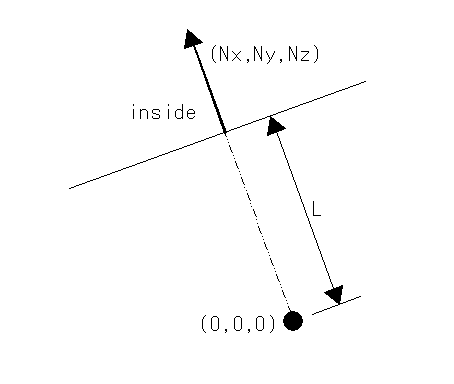
基準点Pを中心に幅Wで側面がベクトルAを向く六角形をベクトルH方向に沿って移動した跡にできる六角形を作成します。
[ 形式 ] Px(1) Py(2) Pz(3) Hx(4) Hy(5) Hz(6) W(7) Ax(8) Ay(9) Az(10)
Px,Py,Pz : 基準点となる円の中心X,Y,Z座標
Hx,Hy,Hz : 円柱の高さ方向のX,Y,Zベクトル (マイナスも入力可。円柱の高さは√(Hx×Hx+Hy×Hy+Hz×Hz)となる)
W : 六角形の幅
Ax,Ay,Az : 側面の一つに垂直なベクトルA (長さは任意)
[入力例]
形状番号1は基準点が(0,0,0)座標から幅3でX軸を向いた六角形がZ軸方向に10伸びた六角柱
形状番号2は基準点が(0,0,0)座標から幅3でX軸を向いた六角形がXとZ軸の間45°方向に14.14伸びた半径2の円柱

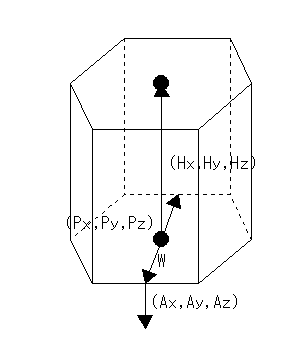
基準点Pを中心にA1、A2、A3ベクトルを軸に持つ楕円を回転させてできる楕円体を作成します。ただし、A1、A2及びA3のベクトルは直行していること。
[ 形式 ] Px(1) Py(2) Pz(3) A1x(4) A1y(5) A1z(6) A2x(7) A2y(8) A2z(9) A3x(10) A3y(11) A3z(12)
Px,Py,Pz : 基準点となる円の中心X,Y,Z座標
A1x,A1y,A1z : 楕円の軸方向を示すX,Y,Zベクトル
A2x,A2y,A2z : 楕円の軸方向を示すX,Y,Zベクトル
A3x,A3y,A3z : 楕円の軸方向を示すX,Y,Zベクトル
[入力例]
形状番号1は基準点が(0,0,0)の楕円体。軸長さは5,4,3
形状番号2は基準点が(0,0,0)の楕円体。軸長さは20,15.3,8.86
